ubuntuへのjuman++、knp、pyknpのインストール方法
jumanのインストール
JUMAN - KUROHASHI-KAWAHARA LAB より最新のjumanのbzip2ファイルをダウンロードし、
$ tar jxvf juman-7.01.tar.bz2 $ cd juman-7.01 $ ./configure --prefix=/home/<username>/.usr $ make $ make install $ ./configure # juman.hをknpインストール時に使うため、prefixを指定しないケースでのインストールも実施する $ make $ sudo make install
そして、jumanを実行できるようにするため、~/.bashrcに以下を記述する。
export PATH=$HOME/.usr/bin:$PATH
また、jumanの*.soファイルを見つけられるように、
$ sudo vim /etc/ld.so.conf
でファイルを開いた後に、以下の1行を追加する。
include /home/<usrname>/.usr/lib
最後にパスを読み込み直す。
$ sudo ldconfig
knpのインストール
KNP - KUROHASHI-KAWAHARA LAB より最新のknpのbzip2ファイルをダウンロードし、
$ tar jxvf knp-4.19.tar.bz2 $ cd knp-4.19 $ ./configure --prefix=/home/<usrname>/.usr --with-juman-prefix=/home/<usrname>/.usr $ make $ make install
juman++のインストール
ku-nlp/jumanpp: Juman++ (a Morphological Analyzer Toolkit)の通り。 Releases · ku-nlp/jumanppより最新のtar.xzファイルをダウンロードし、
$ tar xf jumanpp-<version>.tar.xz # decompress the package $ cd jumanpp-<version> # move into the directory $ mkdir bld # make a subdirectory for build $ cd bld $ cmake .. -DCMAKE_BUILD_TYPE=Release -DCMAKE_INSTALL_PREFIX=/home/<usrname>/.usr $ make install -j<parallelism>
pyknpのインストール
$ pip install pyknp
インストール確認
ターミナルから
$ echo "麻生太郎はコーヒーを買って飲んだ。" | jumanpp | knp -simple -anaphora
と叩いて、以下のように出力されたら成功。
# S-ID:1 KNP:4.19-CF1.1 DATE:2019/06/08 SCORE:-16.31767 * 3D <体言> + 1D <体言><EID:0> 麻生 あそう 麻生 名詞 6 人名 5 * 0 * 0 "人名:日本:姓:135:0.00166 疑似代表表記 代表表記:麻生/あそう" <NE:PERSON:B> + 4D <体言><NE:PERSON:麻生太郎><Wikipediaエントリ:麻生太郎><EID:1> 太郎 たろう 太郎 名詞 6 人名 5 * 0 * 0 "人名:日本:名:45:0.00106 疑似代表表記 代表表記:太郎/たろう" <Wikipediaエントリ:麻生太郎:0-1><NE:PERSON:E> は は は 助詞 9 副助詞 2 * 0 * 0 NIL * 3D <体言> + 4D <体言><EID:2> コーヒー こーひー コーヒー 名詞 6 普通名詞 1 * 0 * 0 "代表表記:珈琲/こーひー ドメイン:料理・食事 カテゴリ:人工物-食べ物" を を を 助詞 9 格助詞 1 * 0 * 0 NIL * 3D <用言:動> + 4D <用言:動><EID:3><項構造:ガ/麻生太郎/1;ヲ/コーヒー/2> 買って かって 買う 動詞 2 * 0 子音動詞ワ行 12 タ系連用テ形 14 "代表表記:買う/かう ドメイン:家庭・暮らし;ビジネス 反義:動詞:売る/うる" * -1D <用言:動> + -1D <用言:動><EID:4><項構造:ガ/麻生太郎/1;ヲ/コーヒー/2> 飲んだ のんだ 飲む 動詞 2 * 0 子音動詞マ行 9 タ形 10 "代表表記:飲む/のむ ドメイン:料理・食事" 。 。 。 特殊 1 句点 1 * 0 * 0 NIL EOS
pythonから
# coding: utf-8 # It is not necessary when you use python3. from __future__ import unicode_literals from pyknp import Juman # default is JUMAN++: Juman(jumanpp=True). if you use JUMAN, use Juman(jumanpp=False) jumanpp = Juman() result = jumanpp.analysis("下鴨神社の参道は暗かった。") for mrph in result.mrph_list(): # 各形態素にアクセス print("見出し:%s, 読み:%s, 原形:%s, 品詞:%s, 品詞細分類:%s, 活用型:%s, 活用形:%s, 意味情報:%s, 代表表記:%s" % (mrph.midasi, mrph.yomi, mrph.genkei, mrph.hinsi, mrph.bunrui, mrph.katuyou1, mrph.katuyou2, mrph.imis, mrph.repnam\ e))
上記スクリプトを実行して、以下のように出力されたら成功。
見出し:下鴨, 読み:しもがも, 原形:下鴨, 品詞:名詞, 品詞細分類:地名, 活用型:*, 活用形:*, 意味情報:自動獲得:Wikipedia Wikipedia地名, 代表表記: 見出し:神社, 読み:じんじゃ, 原形:神社, 品詞:名詞, 品詞細分類:普通名詞, 活用型:*, 活用形:*, 意味情報:代表表記:神社/じんじゃ ドメイン:文化・芸術 カテゴリ:場所-施設 地名末尾, 代表表記:神社/じんじゃ 見出し:の, 読み:の, 原形:の, 品詞:助詞, 品詞細分類:接続助詞, 活用型:*, 活用形:*, 意味情報:NIL, 代表表記: 見出し:参道, 読み:さんどう, 原形:参道, 品詞:名詞, 品詞細分類:普通名詞, 活用型:*, 活用形:*, 意味情報:代表表記:参道/さんどう ドメイン:文化・芸術 カテゴリ:場所-施設, 代表表記:参道/さんどう 見出し:は, 読み:は, 原形:は, 品詞:助詞, 品詞細分類:副助詞, 活用型:*, 活用形:*, 意味情報:NIL, 代表表記: 見出し:暗かった, 読み:くらかった, 原形:暗い, 品詞:形容詞, 品詞細分類:*, 活用型:イ形容詞アウオ段, 活用形:タ形, 意味情報:代表表記:暗い/くらい, 代表表記:暗い/くらい 見出し:。, 読み:。, 原形:。, 品詞:特殊, 品詞細分類:句点, 活用型:*, 活用形:*, 意味情報:NIL, 代表表記:
参考URL
- JUMAN - KUROHASHI-KAWAHARA LAB
- KNP/インストール方法 - KUROHASHI-KAWAHARA LAB
- KNP - KUROHASHI-KAWAHARA LAB
- Ubuntu 日本語形態素解析システムJUMANのインストール方法 | トライフィールズ
- ku-nlp/jumanpp: Juman++ (a Morphological Analyzer Toolkit)
- ku-nlp/pyknp: A Python Module for JUMAN++/KNP
- pyknp: Python Module for JUMAN++/KNP — pyknp documentation
pytorchの誤差関数についてまとめた
pytorchで
- 最後の層の活性化関数
- 誤差関数
の適切な組み合わせについて度々わからなくなってその都度調べているので、ここでまとめておく。
2クラス分類
これは、sigmoidをつけているかどうかで2通りしかない。
| 活性化関数 | 損失関数 | yに対する成約 | 備考 |
|---|---|---|---|
| out = torch.sigmoid(x) | nn.BCELoss() | outと同じdtype・shapeにする | Binary Cross Entropy Loss |
| out = x (活性化関数なし) |
nn.BCEWithLogitsLoss() | outと同じdtype・shapeにする |
多クラス分類
ここがちょっとややこしい。
| 活性化関数 | 損失関数 | yに対する成約 | 備考 |
|---|---|---|---|
| out = F.log_softmax(x, dim=-1) | nn.NLLLoss() | dtype=torch.int64、 shape=(n_samples, ) にする |
Negative Log Likelihood Loss |
| out = x (活性化関数なし) |
nn.CrossEntropyLoss() | dtype=torch.int64、 shape=(n_samples, ) にする |
公式ドキュメントより。 This criterion combines nn.LogSoftmax() and nn.NLLLoss() in one single class. |
基本的にpytorchでF.softmaxは使わないものと思ったら良い。
参考URL
pytorchのチュートリアル集
やはり流石にtensorflowやkerasに比べると数は少ない印象を受けた。
公式
- Welcome to PyTorch Tutorials — PyTorch Tutorials 1.1.0.dev20190425 documentation
- 公式サイト上にあるチュートリアルです。
- pytorch/examples: A set of examples around pytorch in Vision, Text, Reinforcement Learning, etc.
- チュートリアルというよりexample集。「pytorchであのネットワークどう書くんだっけ」と思ったらまずここから探してみる。
その他githubより
- yunjey/pytorch-tutorial: PyTorch Tutorial for Deep Learning Researchers
- この中で一番星の数が多かった。
- MorvanZhou/PyTorch-Tutorial: Build your neural network easy and fast
- この中で唯一notebookで書かれたスクリプトも含まれている。
- hunkim/PyTorchZeroToAll: Simple PyTorch Tutorials Zero to ALL!
- だいぶ基礎的なところから。これはちょっと優先順位低めか。
- spro/practical-pytorch: PyTorch tutorials demonstrating modern techniques with readable code
- まさに表題の通り。pytorch使って実用的なことをやろうと思っているときには、ここのスクリプトをヒントにすると良い。
keynoteで「行頭記号」をつける/消すショートカット
keynoteで「行頭記号」、つまりリスト表記をつける/消すショートカットの紹介。

ショートカットの設定方法
結論から言うと、そのようなショートカットはデフォルトでは存在しない。
自分で設定する必要がある。
右側のカラムにおいて「テキスト」を選択し、「箇条書きとリスト」のプルダウンメニューを選択。
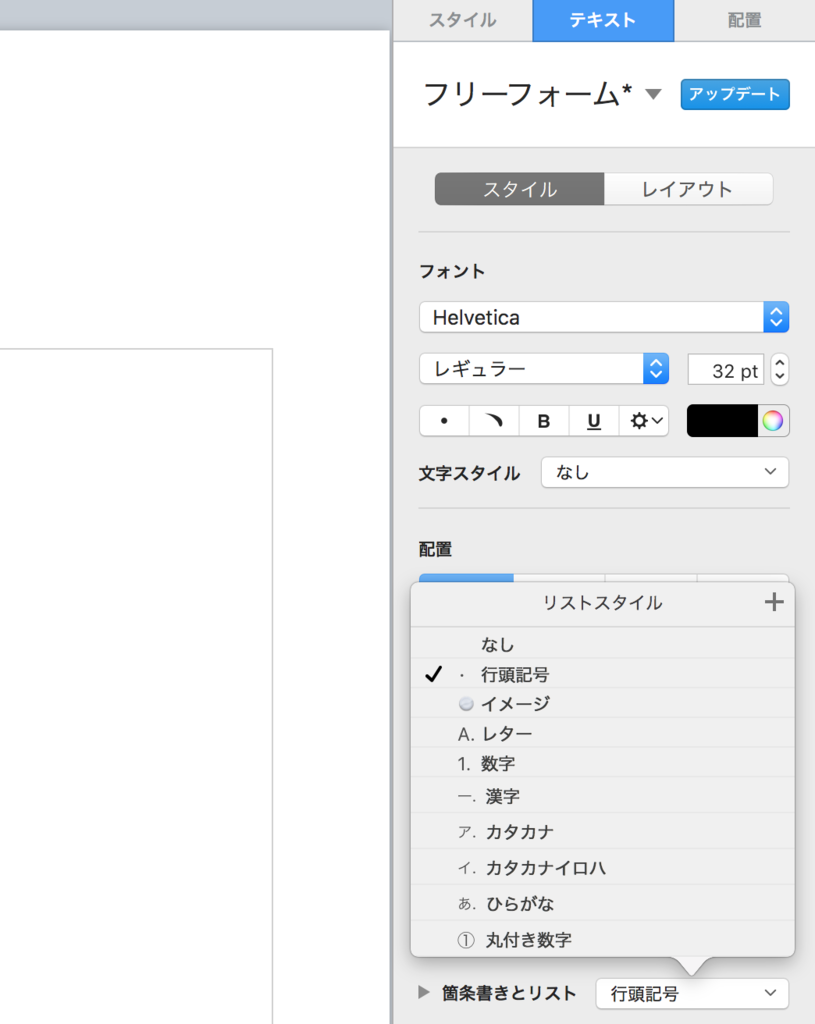
「行頭記号」というところにマウスをかざすと右向きの矢印が出てくるので、そこにカーソルを持っていく。
すると新たにポップアップ画面が表示されるので、「ショートカット」を選択。
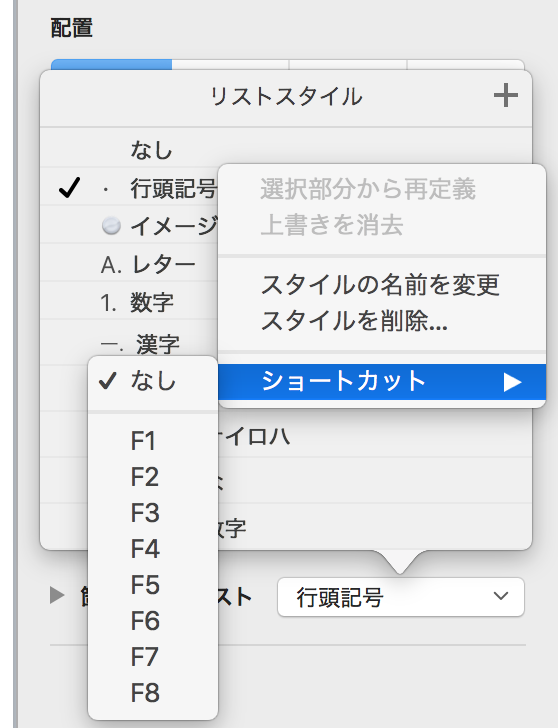
F1からF8が表示されるので、この中からショートカットに割り当てたいものを選択すれば良い。
この設定以降は、割り当てたキーにて「行頭記号」のつける/消す処理が可能となる。
PRMLの目次
上巻
第1章 序論
1.1 例:多項式曲線フィッティング
1.2 確率論
1.2.1 確率密度
1.2.2 期待値と分散
1.2.3 ベイズ確率
1.2.4 ガウス分布
1.2.5 曲線フィッティング再訪
1.2.6 ベイズ曲線フィッティング
1.3 モデル選択
1.4 次元の呪い
1.5 決定理論
1.5.1 誤識別率の最小化
1.5.2 期待損失の最小化
1.5.3 棄却オプション
1.5.4 推論と決定
1.5.5 回帰のための損失関数
1.6 情報理論
1.6.1 相対エントロピーと相互情報量
演習問題
第2章 確率分布
2.1 二値変数
2.1.1 ベータ分布
2.2 多値変数
2.2.1 ディリクレ分布
2.3 ガウス分布
2.3.1 条件付きガウス分布
2.3.2 周辺ガウス分布
2.3.3 ガウス変数に対するベイズの定理
2.3.4 ガウス分布の最尤推定
2.3.5 逐次推定
2.3.6 ガウス分布に対するベイズ推論
2.3.7 スチューデントのt分布
2.3.8 周期変数
2.3.9 混合ガウス分布
2.4 指数型分布族
2.4.1 最尤推定と十分統計量
2.4.2 共役事前分布
2.4.3 無情報事前分布
2.5 ノンパラメトリック法
2.5.1 カーネル密度推定法
2.5.2 最近傍法
演習問題
第3章 線形回帰モデル
3.1 線形基底関数モデル
3.1.1 最尤推定と最小二乗法
3.1.2 最小二乗法の幾何学
3.1.3 逐次学習
3.1.4 正則化最小二乗法
3.1.5 出力変数が多次元の場合
3.2 バイアス-バリアンス分解
3.3 ベイズ線形回帰
3.3.1 パラメータの分布
3.3.2 予測分布
3.3.3 等価カーネル
3.4 ベイズモデル比較
3.5 エビデンス近似
3.5.1 エビデンス関数の評価
3.5.2 エビデンス関数の最大化
3.5.3 有効パラメータ数
3.6 固定された基底関数の限界
演習問題
第4章 線形識別モデル
4.1 識別関数(判別関数)
4.1.1 2クラス
4.1.2 多クラス
4.1.3 分類における最小二乗
4.1.4 フィッシャーの線形判別
4.1.5 最小二乗との関連
4.1.6 多クラスにおけるフィッシャーの判別
4.1.7 パーセプトロンアルゴリズム
4.2 確率的生成モデル
4.2.1 連続値入力
4.2.2 最尤解
4.2.3 離散特徴
4.2.4 指数型分布族
4.3 確率的識別モデル
4.3.1 固定基底関数
4.3.2 ロジスティック回帰
4.3.3 反復再重み付け最小二乗
4.3.4 多クラスロジスティック回帰
4.3.5 プロビット回帰
4.3.6 正準連結関数
4.4 ラプラス近似
4.4.1 モデルの比較とBIC
4.5 ベイズロジスティック回帰
4.5.1 ラプラス近似
4.5.2 予測分布
演習問題
第5章 ニューラルネットワーク
5.1 フィードフォワードネットワーク関数
5.1.1 重み空間対称性
5.2 ネットワーク訓練
5.2.1 パラメータ最適化
5.2.2 局所二次近似
5.2.3 勾配情報の利用
5.2.4 勾配降下最適化
5.3 誤差逆伝播
5.3.1 誤差関数微分の評価
5.3.2 単純な例
5.3.3 逆伝播の効率
5.3.4 ヤコビ行列
5.4 ヘッセ行列
5.4.1 対角近似
5.4.2 外積による近似
5.4.3 ヘッセ行列の逆行列
5.4.4 有限幅の差分による近似
5.4.5 ヘッセ行列の厳密な評価
5.4.6 ヘッセ行列の積の高速な計算
5.5 ニューラルネットワークの正則化
5.5.1 無矛盾なガウス事前分布
5.5.2 早期終了
5.5.3 不変性
5.5.4 接線伝播法
5.5.5 変換されたデータを用いた訓練
5.5.6 たたみ込みニューラルネットワーク
5.5.7 ソフト重み共有
5.6 混合密度ネットワーク
5.7 ベイズニューラルネットワーク
5.7.1 パラメータの事後分布
5.7.2 超パラメータ最適化
5.7.3 クラス分類のためのベイズニューラルネットワーク
演習問題
付録A データ集合
付録B 確率分布の一覧
付録C 行列の性質
付録D 変分法
付録E ラグランジュ乗数
上巻のための参考文献
和文索引
英文索引
下巻
第6章 カーネル法
6.1 双対表現
6.2 カーネル関数の構成
6.3 RBFネットワーク
6.3.1 Nadaraya-Watsonモデル
6.4 ガウス過程
6.4.1 線形回帰再訪
6.4.2 ガウス過程による回帰
6.4.3 超パラメータの学習
6.4.4 関連度自動決定
6.4.5 ガウス過程による分類
6.4.6 ラプラス近似
6.4.7 ニューラルネットワークとの関係
演習問題
第7章 疎な解を持つカーネルマシン
7.1 最大マージン分類器
7.1.1 重なりのあるクラス分布
7.1.2 ロジスティック回帰との関係
7.1.3 多クラスSVM
7.1.4 回帰のためのSVM
7.1.5 計算論的学習理論
7.2 関連ベクトルマシン
7.2.1 回帰問題に対するRVM
7.2.2 疎性の解析
7.2.3 分類問題に対するRVM
演習問題
第8章 グラフィカルモデル
8.1 ベイジアンネットワーク
8.1.1 例:多項式曲線フィッティング
8.1.2 生成モデル
8.1.3 離散変数
8.1.4 線形ガウスモデル
8.2 条件付き独立性
8.2.1 3つのグラフの例
8.2.2 有向分離(D分離)
8.3 マルコフ確率場
8.3.1 条件付き独立性
8.3.2 分解特性
8.3.3 例:画像のノイズ除去
8.3.4 有向グラフとの関係
8.4 グラフィカルモデルにおける推論
8.4.1 連鎖における推論
8.4.2 木
8.4.3 因子グラフ
8.4.4 積和アルゴリズム
8.4.5 max-sumアルゴリズム
8.4.6 一般のグラフにおける厳密推論
8.4.7 ループあり確率伝播
8.4.8 グラフ構造の学習
演習問題
第9章 混合モデルとEM
9.1 K-meansクラスタリング
9.1.1 画像分割と画像圧縮
9.2 混合ガウス分布(Mixtures of Gaussians)
9.2.1 最尤推定
9.2.2 混合ガウス分布のEMアルゴリズム
9.3 EMアルゴリズムのもう一つの解釈
9.3.1 混合ガウス分布再訪
9.3.2 K-meansとの関連
9.3.3 混合ベルヌーイ分布
9.3.4 ベイズ線形回帰に関するEMアルゴリズム
9.4 一般のEMアルゴリズム
演習問題
第10章 近似推論法
10.1 変分推論
10.1.1 分布の分解
10.1.2 分解による近似のもつ性質
10.1.3 例:一変数ガウス分布
10.1.4 モデル比較
10.2 例:変分混合ガウス分布
10.2.1 変分事後分布
10.2.2 変分下界
10.2.3 予測分布
10.2.4 混合要素数の決定
10.2.5 導出された分解
10.3 変分線形回帰
10.3.1 変分分布
10.3.2 予測分布
10.3.3 変分下界
10.4 指数型分布族
10.4.1 変分メッセージパッシング
10.5 局所的変分推論法
10.6 変分ロジスティック回帰
10.6.1 変分事後分布
10.6.2 変分パラメータの最適化
10.6.3 超パラメータの推論
10.7 EP法
10.7.1 例:雑音データ問題
10.7.2 グラフィカルモデルとEP法
演習問題
第11章 サンプリング法
11.1 基本的なサンプリングアルゴリズム
11.1.1 標準的な分布
11.1.2 棄却サンプリング
11.1.3 適応的棄却サンプリング
11.1.4 重点サンプリング
11.1.5 SIR
11.1.6 サンプリングとEMアルゴリズム
11.2 マルコフ連鎖モンテカルロ
11.2.1 マルコフ連鎖
11.2.2 Metropolis-Hastingsアルゴリズム
11.3 ギブスサンプリング
11.4 スライスサンプリング
11.5 ハイブリッドモンテカルロアルゴリズム
11.5.1 力学系
11.5.2 ハイブリッドモンテカルロアルゴリズム
11.6 分配関数の推定
演習問題
第12章 連続潜在変数
12.1 主成分分析
12.1.1 分散最大化による定式化
12.1.2 誤差最小化による定式化
12.1.3 主成分分析の応用
12.1.4 高次元データに対する主成分分析
12.2 確率的主成分分析
12.2.1 最尤法による主成分分析
12.2.2 EMアルゴリズムによる主成分分析
12.2.3 ベイズ的主成分分析
12.2.4 因子分析
12.3 カーネル主成分分析
12.4 非線形潜在変数モデル
12.4.1 独立成分分析
12.4.2 自己連想ニューラルネットワーク
12.4.3 非線形多様体のモデル化
演習問題
第13章 系列データ
13.1 マルコフモデル
13.2 隠れマルコフモデル
13.2.1 HMMの最尤推定
13.2.2 フォワード-バックワードアルゴリズム
13.2.3 HMMの積和アルゴリズム
13.2.4 スケーリング係数
13.2.5 Viterbiアルゴリズム
13.2.6 隠れマルコフモデルの拡張
13.3 線形動的システム
13.3.1 LDSにおける推論
13.3.2 LDSの学習
13.3.3 LDSの拡張
13.3.4 粒子フィルタ
演習問題
第14章 モデルの結合
14.1 ベイズモデル平均化
14.2 コミッティ
14.3 ブースティング
14.3.1 指数誤差の最小化
14.3.2 ブースティングのための誤差関数
14.4 木構造モデル
14.5 条件付き混合モデル
14.5.1 線形回帰モデルの混合
14.5.2 ロジスティックモデルの混合
14.5.3 混合エキスパートモデル
演習問題
下巻のための参考文献
訳者あとがき
和文索引
英文索引
参考
海水の塩分について
海水の塩分ってどれくらい?

(画像はhttp://ocean.fs.a.u-tokyo.ac.jp/forpublica2.htmlより引用)
上図は、1年間で平均した海面塩分の値を示しています。
単位は‰(%の十分の一)です(現代の海洋物理学では、塩分の単位に‰の代わりにpsuを用いることが多いです[後述])。
この図を見ると、場所によって異なりますが、だいたい平均すると海水には大体3~4%程度の塩分が含まれているということが分かります。
一番塩分が低い場所(例えばインド亜大陸の東に位置するベンガル湾や、太平洋の経度帯における北極海など)でおおよそ30‰、それに対して一番塩分が高い場所(例えばインド亜大陸の西に位置するアラビア海や、亜熱帯大西洋、地中海など)でおおよそ40‰です。
これを聞くと、「塩分て世界中の海でだいたいどこも一緒なんやなあ」という感想を持たれる方も多いでしょう。
確かに、塩分の3%と4%の違いなんて、人間の味覚からしたら本当に微々たる違いです。
恐らく「舐めて3%の塩水か4%の塩水か分かる」という人間は一流シェフでもなかなかいないでしょう。
しかし、海に関しては、この1%はおろか、1‰ の違いが、地球の気候に変動を及ぼす可能性すらあるのです。
詳しくはまた時間があるときに書きたいと思います。
海水の塩分の単位「psu」って何?
psuとはズバリ、「Practical Salinity Unit」の略です。直訳すると「実用塩分単位」。
この単位が一体何を表しているのかを理解するために、まずは海水の塩分測定の歴史を紐解いてみましょう。
従来、塩分は海水に溶けている固形物質の質量(g)と海水の質量(kg)との比であると定義されておりました。単位はg/kgすなわち千分率(‰ :パーミル)でした。
つまり塩素の化学的定量によって塩分を求めていたわけですね。
因みに、このように海水の塩分を「海水1kg に塩分がどれくらい含まれているか」で表したものを、「絶対塩分(Absolute Salinity)」と言います。
ところが、化学的定量には手間がかかり、しかも正確に測定するのも難しいというのが現状でした。
そのため、1960年代に液体用の電気伝導率計が発達すると、塩分濃度は電気伝導率で計測するようになりました。
しばらくは電気伝導率から塩分濃度へ換算するという方法をとっていましたが、次第に精度の高い変換をするということが難しいということがわかってきました。
そこで、塩分濃度に換算するという方法を諦め、測定した電導度そのものの数値を塩分とすることになり、1982年以降はその数値を「実用塩分(Practical Salinity)」と呼ぶことになりました。
もう現代では、海水に関して塩分濃度と電気伝導率を関連づける式は存在しません。
矛盾しているように聞こえるかもしれませんが、実用塩分には単位がありません。psuと言うのは電気伝導率の単位ではないのです。
どういうことかというと、実際に計測された海水の電気伝導率そのものが実用塩分(psu)というわけではなく、その電気伝導率と「塩化カリウムの標準液」の電気伝導率の比を実用塩分と呼んでいるのです。
ですから、敢えて「実用塩分の単位って何?」という問いに応えるとしたら、それは‰になります。
しかしその意味合いは絶対塩分の単位‰とは全く異なります。普通、実用塩分の単位に‰は用いません。
「これは絶対塩分ではなくて実用塩分の値ですよ!」ということを明示するために、psuという文字列を単位のように使っているのです。
なので、「実用塩分の単位はpsuである」というのは、実は正式なものではないのです。
で、このページの上部に掲載してある塩分分布、単位が‰になっていますね。つまりこれは絶対塩分で表した分布ということになります。
「今は絶対塩分じゃなくて実用塩分を使っているんやろ? じゃあ実用塩分で書かれた図を見せろや」という主張がもしかしたらあるかもしれません。
しかしご安心を。実用塩分(psu)と絶対塩分(‰)は、数値としてはほとんど一緒の値を示すのです。というか、そのようになるように実用塩分を設定したのです。
もっと詳しく言うと、実用塩分値35(psu)は、絶対塩分値35(‰)と同等です。そして35psu以外の塩分についても、実用塩分(psu)と絶対塩分(‰)の数値の差は非常に小さくなっております。
ですから、逆に単位psuで書かれた塩分マップが手元にあるとき、例えば36psuの塩分の海水は「だいたい36‰の塩分濃度である、つまり海水1kgあたり36gの塩分が含まれているような濃度である」と考えて差し支えはありません。
引用文献
日本の大学院進学率
日本全体の大学院進学率は約12~13%
※この記事においては、「大学の学部を卒業した人のうち、大学院に進学した人の割合」を大学院進学率と定義しているのでご注意ください。
日本の大学院の進学率は、どれくらいのものなのだろう?
例えば京都大学だけで見ると、平成二十八年の大学院進学率は58%(学部卒業生2931人中、大学院に進学した人が1707人)であった。
(参考:http://www.kyoto-u.ac.jp/ja/about/data/careers.html)
しかし日本全体の大学院進学率に関するデータはなかなか見当たらない。
というわけで詳しく調べてみることにした。
すると、文部科学省のページ(平成25年度博士・修士・専門職学位の学位授与状況)に以下のような数字が。
平成二十五年の修士の学位授与数は、74,187件
つまり、日本における修士課程在籍者の1学年あたりの人数は、約7~8万人ということになる。
1学年あたりの大学生の人数が約60万人(日本の1学年あたりの人数が約120万人で、大学進学率が約50%)と大雑把に考えると、日本全体での大学院進学率は、
7~8(大学院進学人数[万人]) / 60(学部卒業人数[万人]) = 約12~13%
という結果となった。
日本においては、全大学生のうち、大学院に進学できる人が8人に1人程度。
自分はとても恵まれていた。